A mathematical description of the observation from the last page, that the amount of diffusion (the diffusion flux) depends on the difference in concentration of the diffusing element (the concentration gradient), is given by:
where J is the diffusion flux (mol/m2/s), C is the concentration (mol/m3), X is the distance (m), and D (m2/s) is the diffusion coefficient. To calculate how the concentration of the diffusing element changes with distance and time, solutions are needed to a partial differential equation:
where t (s) is the time. Analytical solutions to this equation for a variety of boundary conditions can be found in Crank (1975). By looking at a couple of those solutions, some understanding of diffusion processes can be extracted without a lot of mathematical work.
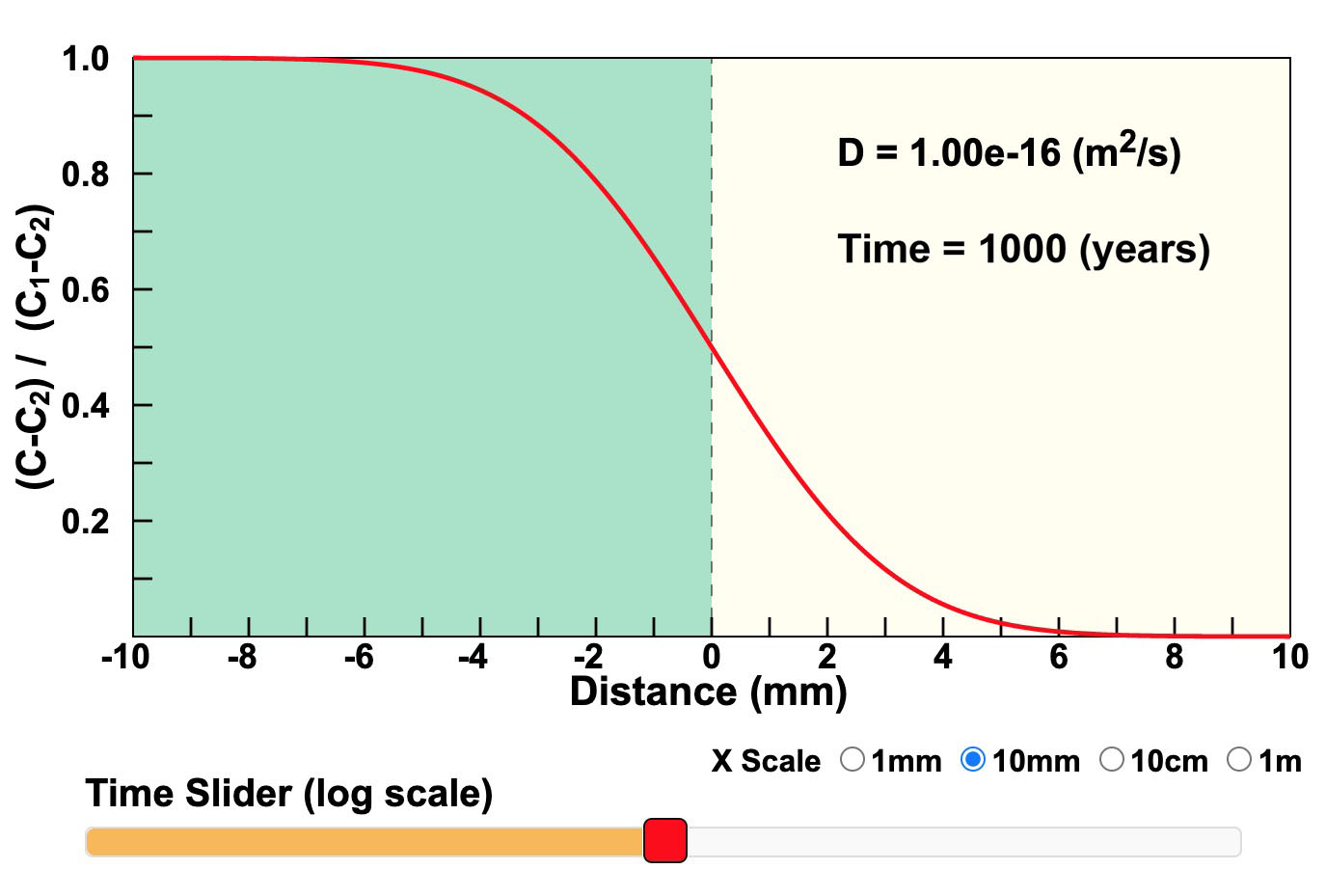
Figure 20. Diffusion Infinite Extent Couple. This diagram shows an exact solution to the diffusion equation given by Crank (1975, equation 2.14) for diffusion across a boundary between two phases of infinite extent. Click on the image for a larger, interactive version where you can observe what happens as time changes.
The first example, shown here as Figure 20, is of diffusion between two phases of infinite extent. This solution shows how far from the boundary that the concentration will change over time without having to think about running out of diffusing atoms. Concentration is shown on the y-axis and distance is on the x-axis with the contact between the two phases in the middle. Concentration has been normalized to begin at 1 for the phase on the left and 0 for the phase on the right. Click on Figure 20 and move the time slider to see the concentrations change as time changes. Notice that the time slider is logarithmic. Fick's First Law says that the flux across the boundary is proportional to the concentration gradient (the slope of the concentration graph) at the boundary. That slope decreases with time, so the quantity of diffusing atoms that move across the boundary decreases with time.
Figure 20 also gives you the option of changing the diffusion coefficient. If the diffusion coefficient is multiplied by 10, the diffusion distance is only multiplied by the square root of 10 (~3.16). The value of the square root of (4Dt) is calculated and shown on the diagram. This value may be used to estimate the effective diffusion distance.