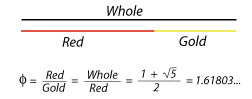
Fibonacci Phyllotaxis - Golden section/Golden Mean - Golden Angle - Golden angle vs. Fibonacci

Fibonacci Numbers - Golden Angle

Many plants display Fibonacci Phyllotaxis, featuring Fibonacci numbers and the Golden Angle. The Golden Angle is related to the Golden Mean, itself a limit of quotients of Fibonacci numbers. We review these facts below. The dynamical model offers an explanation of why Fibonacci phyllotaxis is so predominant. To find out more about the Fibonacci numbers and the Golden Mean, visit Ron Knott's web site.

Fibonacci Phyllotaxis
 

In spiral phyllotaxis, the number of visible spirals, called parastichies, are most often two successive elements of the Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...
where each number is the sum of the previous two. When this occurs, the angle between successive leaves or botanical element is close to the Golden Angle - about 137.5o, related to the golden mean.

The Aonium on the right exhibits 3 spirals winding in one direction, 2 in the other. The angle between leaves 2 and 3 and the angle between leaves 5 and 6 are both very close to 137.5o.
 

 

Based on a survey of the literature encompassing 650 species and 12500 specimens, R. Jean (1994) estimated that, among plants displaying spiral or multijugate phyllotaxis about 92% of them have Fibonacci phyllotaxis.

   
Golden Section and Golden Mean

Return to Top
 

 

The Greeks knew that to draw the pentagram, one has to divide a segment in the Golden Section. The Golden Section is the only way to divide a segment so that the ratio of the large segment (Red here) over the small (Gold) is the same as the ratio of the whole segment (Whole) over the large (Red). This ratio is the Golden Mean Ø (phi):

  
 
 
Golden Section and Golden Angle

Return to Top
 

One obtains the Golden Angle, of about 137.51 degrees, by a golden section of the circumference of the circle:

    
 
 
Fibonacci Numbers and Golden Mean
 

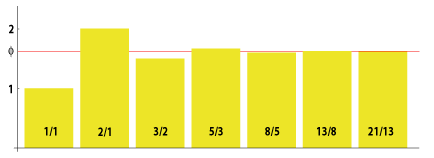
The Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34 etc. is given by the recurrent relation Fn+1= Fn + Fn-1 (each term is the sum of the two previous ones), with initial condition F0= F1=1.

The Golden Mean is a limit of quotients of successive Fibonacci numbers:

technically: Ø = lim Fn/Fn-1 as n goes to infinity (proof below)

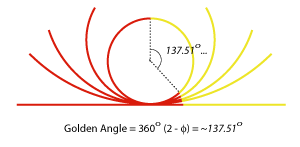
In the same way, the Golden Angle is given by the limit of quotients of Fibonacci numbers that are two appart:

Golden Angle = 360(2- Ø) = 360 lim Fn/Fn+2

(proof below) So it is not surprising that the Fibonacci numbers and the Golden Angle arise at the same time in plants. But this is not an explanation of why and how they do arise. The dynamical model does provide an explanation, given general assumptions about the pattern formation mechanism.

 
 

Return to Top

- To get the value of Ø from the golden section definition given above, set Whole=x and Red=1. Then Gold=x-1 and the equality Ø= Whole/Red = Red/Gold becomes Ø= x = 1/(x-1), from which we obtain x(x-1)=1, or x2-x-1=0. Using the quadratic formula, one finds that Ø = x = (1+sqrt(5))/2 is the only positive root of this equation.

- To prove that the Golden mean is a limit of quotients of Fibonacci numbers, assume that lim Fn/Fn-1= L . We will show L= Ø. Divide the equality Fn+1= Fn + Fn-1 by Fn to get Fn+1/Fn = 1+Fn-1/Fn. Taking the limit as n goes to infinity yields L = 1+1/L or L2-L-1=0, which has the only positive root L= Ø. A more rigorous proof would not assume that L exists, as we did, but would start with proving the equality (1-Ø)n= Fn+1-Fn*Ø by induction.

- To show that (2- Ø) = lim Fn/Fn+2 , divide Fn+1= Fn + Fn-1 by Fn+1 and proceed as before.

 

Fibonacci Phyllotaxis - Golden section/Golden Mean - Golden Angle - Golden angle vs. Fibonacci