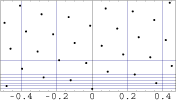




ClassificationThe four main types of phyllotaxis usually recognized are shown below. They can be detected and further classified by the number of visible spirals (parastichies) they display. All these patterns can be modeled by simple lattice-like mathematical structures. Spiral phyllotaxis is the most frequent. Other patterns may exist that are not quite as regular, and seldom mentioned by botanists.
|
||||||||||||
Distichous Phyllotaxis |
Whorled Phyllotaxis |
|||||||||||
 |
|
 |
 |
|
 |
|||||||
| In distichous phyllotaxis, leaves or other botanical elements grow one by one, each at 180 degrees from the previous one. |
In whorled phyllotaxis, two or more (three in the example above) elements grow at the same node on the stem. Elements in a node are evenly spread around the stem, midway between those in the previous node. |
|||||||||||
Spiral Phyllotaxis |
Multijugate Phyllotaxis |
|||||||||||
 |
|
 |
 |
|||||||||
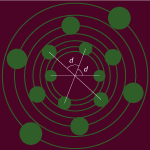
| In spiral phyllotaxis, botanical elements grow one by one, each at a constant divergence angle d from the previous one. This is the most common pattern, and most often the divergence angle d is close to the Golden Angle, which is about 137.5 degrees. The latter case gives rise to Fibonacci Phyllotaxis. |
In multijugate phyllotaxis, two or more botanical elements (two
in the example above) grow at the same node. Elements in a whorl
(group of elements at a node) are spread evenly around the stem
and each whorl is at a constant divergence angle d from
the previous one. Often, multijugate patterns look very similar
to spiral patterns and the only way to detect them is to count the
number of spirals visible in the pattern (see below). |
|||||||||||
|
|
||||||||||||
| To further classify spiral and multijugate patterns, one counts the number of visible spirals, called parastichies, which join each element to its nearest neighbors. These spirals normally come in two families, yielding a pair of numbers, called parasitichy numbers. If the parastichy numbers have no common divisor other than 1, the pattern is a spiral phyllotaxis. If the parastichy numbers do have a common divisor k, then the pattern is multijugate (more precisely k-jugate) and there are k elements at each node. The notion of parastichy numbers can be extended to distichous phyllotaxis with parastichy numbers (1,1) and whorled with parastichy numbers (k,k).
|
||||||||||||
 |
 |
 |
 |
|||||||||
| This Aonium has parastichy numbers (2, 3). Since 1 is the only common divisor of 2 and 3, this is a spiral pattern. Since spiral phyllotaxis can be viewed as 1-jugate, the notation 1(2,3) is also used for this pattern.
|
This gymnocalycium has parastichy numbers
|
|||||||||||
The classification of a phyllotactic pattern (from the 4 above kinds) is given by its pair of parastichy numbers (m,n). If k is the greatest common divisor of m and n, and m=ki, n=kj, the notation k(i, j) may be used. The number k is the number of elements per whorl. When k =1, the configuration is called spiral, when k>1 and i=j, it is whorled or k-merous and when k>1, and i, j are distinct, it is called multijugate (and more specifically k-jugate). As special cases, (1, 1) configurations are called distichous, and 2-whorled (or dimerous) patterns, 2(1,1) are called decussate. The configuration is a Fibonacci phyllotaxis when the parastichy numbers are successive elements in the Fibonacci sequence. To learn more about spiral phyllotaxis and parastichies, visit the spiral lattice page.
Spiral phyllotaxis is the most common kind of phyllotactic pattern. According to a survey by Hutchinson (see Meicenheimer (1998)), in a sample of 650 dycotyledonous families, 50.6% showed exclusively spiral or multijugate phyllotaxis, 14.7% showed exclusively whorled phyllotaxis while 34.7% showed a mixture of these phyllotaxes. According to a compilation by Jean (1994) of many surveys of 650 species and 12500 specimens, among plants showing spiral or multijugate phyllotaxis, about 92% showed Fibonacci phyllotaxis (with parastichy numbers successive elements in the Fibonacci sequence), 6% where bijugate 2(i,j) with i and j successive Fibonacci numbers, 1.5% were spiral phyllotaxis with Lukas parastichy numbers (Lukas numbers form a Fibonacci-like sequence starting at 1, 3. Lukas gave the Fibonacci numbers their name in the 19th Century).
|
||||||||||||
Other Phyllotactic Patterns |
||||||||||||
|
One of the findings with the dynamical model presented in this site is that there might be phyllotactic patterns that show a regularity not of any of the above 4 kinds. In these other patterns, that we have named periodic orbits, the divergence angle is not constant but repeats periodically a finite sequence of values. There is some evidence for the existence of such patterns in plants. Note how the example shown below resembles a regular lattice and seems to display families of parastichies (mathematically, this pattern can be obtained by superimposing 2 lattices). However, in one family, these "parastichies" are undulating. Nonetheless, this superficial similarity with lattice patterns may be the reason why periodic orbits are usually not recognized by botanists.
|
||||||||||||
|
A periodic orbit of period 2 for the dynamical model, with divergence angles 174.35 and 55.12 degrees that repeat indefinitely. This is a (unrolled) cylindrical representation of phyllotaxis. |
|
|||||||||||
Classification - Counting spirals - In a nutshell - Frequency of patterns - Other patterns |