



|
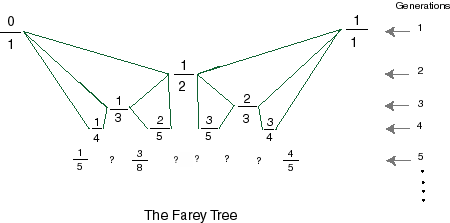
1. Observing Spiral Patterns > 2. Spiral Applet > 3. Dynamical Model Applet > 4. Cylindrical Spirals > 5. Cylindrical Spirals Applet> 6.The Farey Tree and the Golden Mean 6. The Farey Tree and the Golden Mean In this section, we try to explain the following observed fact: the divergence angle in plants is overwhelmingly often close to either 222.5 degrees or 360-222.5=137.5 degrees. You can check that in the leaves of many plants. We will see that these angles are related to the golden mean (which we will discover in this section) and the Fibonacci sequence. ( Remember that the divergence angle is the angle a , which you use to draw spirals in 1. Observing Spiral Patterns or in 4. Cylindrical Spirals .) In the previous section, you filled up the different regions in the parameter space with pairs of parastichy numbers. You might have noticed that there is a definite pattern in the way these numbers appear. It turns out that, in a way that is not quite direct (for now) this pattern is an expression of a construction that mathematicians call the Farey Tree.
Task 33: Note that each fraction in the Farey tree has two "parents" in generations above (e.g., 3/5 has parents 1/2 and 2/3). What is the rule to find the "child" fraction knowing its two parents? Find the fractions that should be where there are question marks. Better still, find the sixth generation of fractions in the Farey tree. Task 34: The Fibonacci path that you found in Task 32, with parastichy numbers (1,2), (2,3), (3,5), .... corresponds to a path of fractions 1/2, 2/3, 3/5, .... in the Farey tree. Is there something remarkable about this path? Use a calculator to compute the decimal values of these fractions (e.g. .5, .6666, .7.5 , ?, ?......). Compute and write down enough of these to find a remarkable pattern/fact. Task 35: The Golden mean is a number which is very popular among architects, painters, musicians and .... plants! (although how recent this fad is in the arts is subject to serious contention.) The computer screen in front of you may have a ration length/height which is close to the golden mean. The Golden mean F is given by the formula F = (1 + sqrt(5))/2 Use a calculator to compute this number. How does it relate to what you observed in the previous task? Sometimes the Golden mean refers to 1/F. What is that number? What is the angle 360 (1/ F)? What is the angle 360-360 (1/ F)? How are these angle related, geometrically? The same specie of plant may choose one or the other. There is apparently a preference depending on which hemisphere the plant grows!
How is all this related to our cylindrical spirals? In Bigger Cylinder Applet turn "partition", "nearest" and "numbers". Look at the set of gray arcs in the parameter space. As you go down one gray arc, it comes to a branching point, with two gray arcs parting and a black one continuing the gray one you were on. To label this branching point, go down the black arc that goes down from it. If you extend this black arc all the way to the bottom (see the arrows on the diagram below), you get to a point on the x- axis. This point is always the base of one of the roundish bowls (regions with only one family of parastichies), and its coordinate is a fraction. If you label this branching point with this fraction you get the Farey tree! You can get the coordinate of this bottom point from the parastichy information as well: As you get down on a gray branch where the parastichy numbers are (2,3), you know the denominator of the fraction attached to the branched point is going to be 2+3=5. To find the numerator, one has to use a little number theory...
In the next few tasks we'll try to unveil more of the relationship between golden mean and the Fibonacci sequence. Task 36: Check, using the quadratic formula that F is a solution of of x2 -x-1=0 .Task 37: We will denote here by Fn the nth term of the Fibonacci sequence. Hence: F1=1, F2=1, F3=2, F4=3, F5=5 , etc.. What is F8? F10? Explain why the Fibonacci sequence can be characterized by :F1=1, F2=1 Fn+2= Fn+1+Fn. Now remark that if we set Fn=xn then Fn+2= Fn+1+Fn. becomes xn+2=xn+1+xn which, dividing by xn simplifies to:x2=x+1 or:x2-x-1=0 The plot thickens!Task 38: 25 bonus points for your group if you follow the above lead and show that, as n becomes very big, Fn/Fn-1 approaches F arbitrarily closely...
1. Observing Spiral Patterns > 2. Spiral Applet > 3. Dynamical Model Applet > 4. Cylindrical Spirals > 5. Cylindrical Spiral Applet > 6. The Farey Tree and the Golden Mean |
||