



|
1. Observing Spiral Patterns > 2. Spiral Applet > 3. Dynamical Model Applet> 4. Cylindrical Spirals > 5. Cylindrical Spirals Applet > 6. The Farey Tree and the Golden Mean Symmetry in Plants A Task-Based Tutorial on the Mathematics of Phyllotaxis
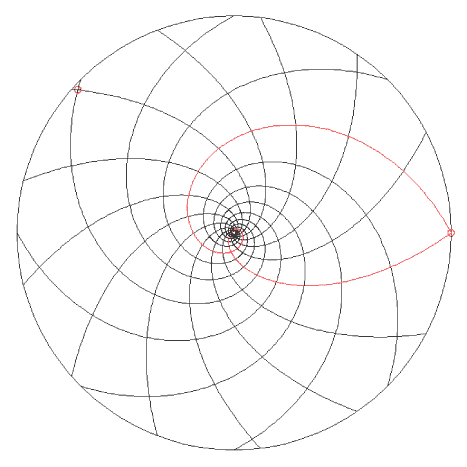
Note: this was part of the "Discovering Math" class taught at Smith College in the Spring of 99. The previous part of the class included studying symmetry of planar patterns. 1. Observing Spiral Patterns In the first part of this tutorial, we get introduced to the patterns and to some of the mathematical models that help analyzing them. Task 1: In looking at the different pictures below, notice that they all have the common trait of exhibiting each two distinct families of spirals. These spirals emanate from the center and wind in opposite directions. In each picture, count the number of spirals in each of the two opposite families. Note that Figures 3 and 4 are mathematically generated. Can you explain how this type relate to botanical patterns of the type seen in Figures 1 and 2 as well as to one another? Which of Figure 3 and 4 seems, to your taste, to better represent botanical patterns?
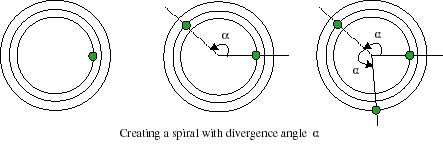
Creating Your Own Spirals In this section, you will need the sheets of concentric circles provided by your instructor (or download them: bigcircle.pdf, tightcircles.pdf), a sharp pencil, a good eraser, scissors and maybe a ruler. Task 2: Using the sheet bigcircle, place one dot on each of the concentric circles so as to form one spiral of dots. What geometric rule do you have to follow to make this spiral look nice and regular? Invent a practical device to implement this rule in a neat way, using paper, scissors, and maybe a ruler (nature is quite precise!).Remark: As you may have observed, there are actually several ways of creating regular spirals by placing one dot per circle. The patterns of Figures 1-4 are obtained by recursively moving a point to the next circle and then rotating it by a fixed angle on that circle. This angle is called divergence angle in botany.
Task 3: Until now in this class, we have defined a symmetry of a figure as a rigid motion (translation, rotation, reflection, and glide reflection) that preserves the figure. Assume that, in Task 2, you have followed the rule described in the previous Remark to draw a regular spiral. If you imagine your spiral going forever inwards as well as outwards, what kind of new motion preserves the spiral?Task 4: Make another spiral on another copy of bigcircle, following the rules described in the remark, striving to spread the points so that they fill the space the most evenly you can (Hint: try playing with the divergence angle a to tighten or loosen your spiral as you would the coiling spring of an old clock). Refrain for now to connect the dots. Once you have done that on bigcircle, do it in the two figures of tightcircles. What artistic device could you use in order for your pattern to look more plant like?Task 5: Look at your artwork from Task 4. Do you see any spirals other than the one you intended to draw? Somehow your eyes may connect the dots of your original spiral in unexpected ways. Do connect some of these dots, enough to show the pattern you perceive. What kind of rules do you follow when connecting the dots in order to form these extra spirals? How many families of such spirals do you detect and how many spirals do you see in each family?You have seen 2 kinds of spirals in your artistic endeavour. The first kind, that you deliberately drew, is called the generative spiral. The dots in this spiral follow all the successive generations of circles and generate spontaneously the second kind of spirals, which often come in families. This second kind of spirals, which you drew in Task 5, is called parastichy. You saw and counted parastichies in Task 1. Task 6: Is it easy to see the generative spirals in Figures 1-4 of Task 1? Why? What does this tell you about how plants form their botanical entities?
1. Observing Spiral Patterns > 2. Spiral Applet > 3. Dynamical Model Applet > 4. Cylindrical Spirals > 5. Cylindrical Spirals Applet> 6. The Farey Tree and the Golden Mean
|
||||||