After computing the visibility graph of a set of obstacles, we have all we need to compute the shortest path from a point pstart to another point pgoal. Dijkstra’s algorithm will now be illustrated.
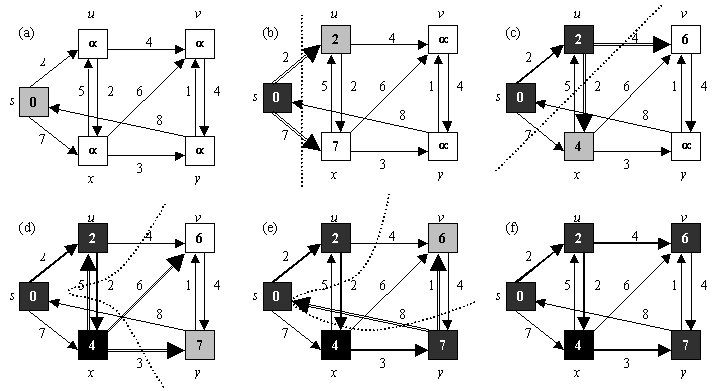
Suppose we have the following graph G = (V,E), where V are the vertices/nodes and E are the edges. Dijkstra’s algorithm requires that the distances between nodes that have an edge between them be known. They are given as numbers on the edges. Suppose we want to find the shortest path from s to v.
The numbers in the boxes will indicate the current shortest path from p to that node. Let d(node) denode this distance. First, we initialize d(s) = 0 because we travel zero distance to go from s to s, and initialize all other d(i) = infinity because no paths have been determined yet. We now define a cut (denoted by a dotted line) to be a line dividing the nodes which shortest distances d(i) have already been determined, and we color such nodes black. Moreover, we color as gray the node which shortest distance from s we are currently determining.

Here is how Dijkstra’s algorithm works. At (a), we start from s, and consider all edges that go to s. This is obviously trivial and d(s) is zero. So the shortest distance to s is determined and we color s as black. At (b), we establish our cut as the dotted line between s and (not s). We consider all the edges that intersect our cut, that is, the two edges which are of lengths 2 (s,u) and 7 (s,x), and are double-lined. We choose the shortest of these edges, (s,u). We look at the d(u) value at u, which is infinity and obviously greater than 2. Therefore, infinity is replaced by 2 as the d(u) value. So u’s shortest distance from s has been determined as well. It is considered to be inside our cut in (c).
In (c), we again consider all the edges that intersect our cut (and have not been considered). Our cut is between s, u, and the rest of the vertices. They are of lengths 4 (u,v) and 2 (u,x) respectively. 6 is smaller than infinity, which therefore gets replaced. Also, 4 is smaller than 7 (the current d(x) value), which also gets replaced. Since (u,x) is shorter than (u,y), it is chosen to be in our set of shortest path edge, and the shortest path of x is determined as well. Note that the slightly darkened edges represent the edges that have been chosen as our list of edges in our shortest path. This process continues until the final shortest distances of all nodes have been found. Since we are using Dijkstra’s algorithm to find the shortest path from one point pstart to another pgoal, we can stop when the shortest path of pgoal has been discovered.
One crucial point about Dijkstra’s algorithm will not be proven here. Whenever we choose the shortest edge (a,b) across a cut, we say that the shortest distance from s to b has already been found. Moreover, the running time of Dijkstra’s algorithm is O(V2 + E), where V is the number of vertices, and E the number of edges. The intuition is that, in a complete graph, when we visit each vertex, we will be considering its distance from V – 1 other vertices. Therefore, O(V2). Moreover, all edges will be ‘touched’ once, and there are E edges. So O(V2 + E). Returning to our original notationals, where n is the number of vertices, and in a complete graph there are O(n2) edges, Dijkstra’s algorithm is O(n2). I will only state these as facts without proving them. The proofs can be found in any textbooks about graph algorithms.
Now
that the shortest path between two points have been found, our whole task
of robot motion planning has been solved.