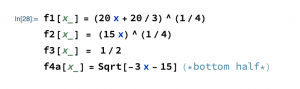From MTH112 to special studiesIn Fall 2021, classes returned to being held in- person, but the impacts of the COVID-19
|
MATHEMATICA AND SOLID OF REVOLUTION |
ROTATED SOLIDSMost students learn in geometry how to calculate the area of a cylinder or a sphere—and these are volumes of revolution! What students aren’t taught, however, is how to calculate the area of a donut, or a water bottle, or any shape that is rotated around an axis. Using calculus, we can find these volumes. To calculate a volume of revolution, imagine slicing the volume into thin disks or cylinders, then finding the sum of the volumes of each disk. As the number of slices and disks increase, the sum more closely approximates the exact volume of the solid. |
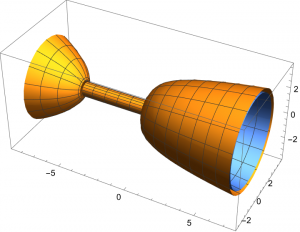
MATHEMATICAPart of the project was to use Mathematica, a mathematics computation and visualization software, to render 3D images of students’ rotated solids. The software’s Parametric Plotting function allowed students to look at different versions of their chalice designs, and seeing a 3D view of a cross section allowed students to create more effective, realistic, and interesting designs. When working with 3D printers, you need to use specific file types. To start the process, we looked first at sample code in Mathematica for producing 3D printed objects – specifically a triceratops! Once we worked out the details of the 3D printing process, we moved on to working with code from student designs. Instead of plotting the surfaces of the solids using ParametricPlot, we needed to create a solid region. One of the built-in commands in Mathematica is RegionPlot3D. After a little tinkering, we managed to take the structure of the student project code and make solids suitable for printing. |
Design Thinking and CFD 3D Printer access at SmithUnknown to many on campus, the Center for Design and Fabrication (CDF) lies tucked within Smith’s campus, accessible through the basement stairs within McConnell Hall. The CDF exists to enhance the experience students have with learning and research through a variety of machinery, welding, fabrication, woodworking and rapid prototyping tools. Interdisciplinary design thinking at Smith is much bigger than most students know of, incorporating design methods through classes, as well as supporting student and faculty-led design projects. The Smith College Makers Map points students in the direction of what’s available for student use, such as the accessibility of having 3D printers in four buildings across campus. The use of these tools is available for any students interested in pursuing a project! |
STEPS
| Combination of Functions:
|
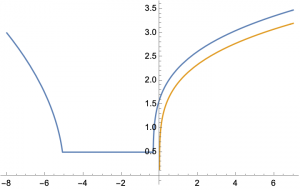
2D plot:
|
|
3D plot:
|
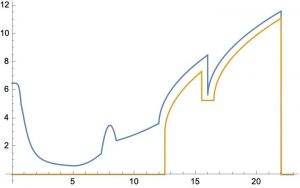
3D Printing:
|
Printed Chalice |
|
Special thanks to Eric Jenson(Center for Design and Fabrication), Nina Peleaz (Smith College Museum of Art), Leslie Fields (Special Collections), the Department of Mathematical Sciences, and the Design for Thinking Initiative.
 pandemic continued for both students and faculties. The faculty teaching MTH112 that semester, at the suggestion of Dr. Candice Price, decided to implement collaborative projects to challenge students and hone their skills rather than the more traditional exam structure. One of the projects that prized creativity was the Chalice of Fire project.
pandemic continued for both students and faculties. The faculty teaching MTH112 that semester, at the suggestion of Dr. Candice Price, decided to implement collaborative projects to challenge students and hone their skills rather than the more traditional exam structure. One of the projects that prized creativity was the Chalice of Fire project.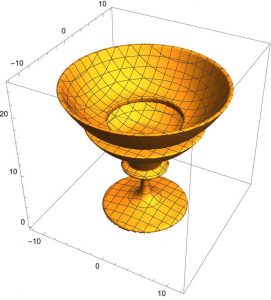 Students in groups of 2-3 were challenged to design chalices as volumes of revolution. The only requirements were that the chalice could hold 150 cm^3 of water but used less than 150 cm3 of material to construct. Students enthusiastically embraced the challenge, designing a whole range of amazing chalices, writing persuasive sales pitches for their designs, and rendering their chalices in Mathematica, computing the volume of material, the volume they could hold, and the center of mass for their individual designs.
Students in groups of 2-3 were challenged to design chalices as volumes of revolution. The only requirements were that the chalice could hold 150 cm^3 of water but used less than 150 cm3 of material to construct. Students enthusiastically embraced the challenge, designing a whole range of amazing chalices, writing persuasive sales pitches for their designs, and rendering their chalices in Mathematica, computing the volume of material, the volume they could hold, and the center of mass for their individual designs.  The creativity on display led students to consider how they could turn these computer- generated designs into solid objects. Along with Dr. Jennifer Beichman, a group of seven students set out to convert the Mathematica code into 3D printed objects, now on display in the Neilson Library Reading Room.
The creativity on display led students to consider how they could turn these computer- generated designs into solid objects. Along with Dr. Jennifer Beichman, a group of seven students set out to convert the Mathematica code into 3D printed objects, now on display in the Neilson Library Reading Room.