Albertson Abstract
Next: Bonin Abstract
Up: Index of Abstracts
Previous: Abstracts of talks
Symmetry Breaking in Graphs
Michael O. Albertson, Department of Mathematics, Smith College
Northampton, MA 01063, albertson@smith.smith.edu
and
Karen Collins,
Department of Mathematics, Wesleyan University
Middletown, CT
06459-0128
kcollins@wesleyan.edu
A classic elementary problem with a surprise answer is the following:
if a circular key ring holds n identically shaped keys, and in order to
tell them apart, we plan to affix to each one a colored label, what is
the minimum number of different colors needed to distinguish the keys?
The surprise is that if
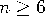 , there
need only be 2 different colors of labels; but if there are three, four,
or five keys on the ring, there must be 3 different colors of labels.
If we consider the keys as vertices in the n-cycle, then the effect
of the labels on the vertices is to destroy every symmetry of the
n-cycle.
, there
need only be 2 different colors of labels; but if there are three, four,
or five keys on the ring, there must be 3 different colors of labels.
If we consider the keys as vertices in the n-cycle, then the effect
of the labels on the vertices is to destroy every symmetry of the
n-cycle.
Define a labeling of a graph G, 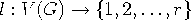 ,
to be r-distinguishing if no automorphism of G
preserves all of the vertex labels. Then a natural question is,
for any graph G, what is the minimum r such that G is
r-distinguished? For an n-cycle, the answer is 3 if
n=3,4,5 and 2 if
,
to be r-distinguishing if no automorphism of G
preserves all of the vertex labels. Then a natural question is,
for any graph G, what is the minimum r such that G is
r-distinguished? For an n-cycle, the answer is 3 if
n=3,4,5 and 2 if 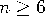 .
For a complete graph on m vertices,
the answer is m. We give a bound on the minimum distinguishing
number of a graph in terms of the order of its automorphism group, as
well as finding the distinguishing numbers of graphs
whose automorphism groups are abelian, dihedral,
.
For a complete graph on m vertices,
the answer is m. We give a bound on the minimum distinguishing
number of a graph in terms of the order of its automorphism group, as
well as finding the distinguishing numbers of graphs
whose automorphism groups are abelian, dihedral, 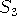 , or
, or 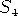 .
.
Thu Sep 14 11:50:14 EDT 1995
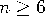 , there
need only be 2 different colors of labels; but if there are three, four,
or five keys on the ring, there must be 3 different colors of labels.
If we consider the keys as vertices in the n-cycle, then the effect
of the labels on the vertices is to destroy every symmetry of the
n-cycle.
, there
need only be 2 different colors of labels; but if there are three, four,
or five keys on the ring, there must be 3 different colors of labels.
If we consider the keys as vertices in the n-cycle, then the effect
of the labels on the vertices is to destroy every symmetry of the
n-cycle.
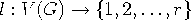 ,
to be r-distinguishing if no automorphism of G
preserves all of the vertex labels. Then a natural question is,
for any graph G, what is the minimum r such that G is
r-distinguished? For an n-cycle, the answer is 3 if
n=3,4,5 and 2 if
,
to be r-distinguishing if no automorphism of G
preserves all of the vertex labels. Then a natural question is,
for any graph G, what is the minimum r such that G is
r-distinguished? For an n-cycle, the answer is 3 if
n=3,4,5 and 2 if 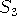 , or
, or 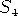 .
.