CSC270  Homework #1 Solution

Resistor circuits

Problem 1

In the circuit shown in Figure 1, what is the voltage between Point A and ground? Between Point B and ground?

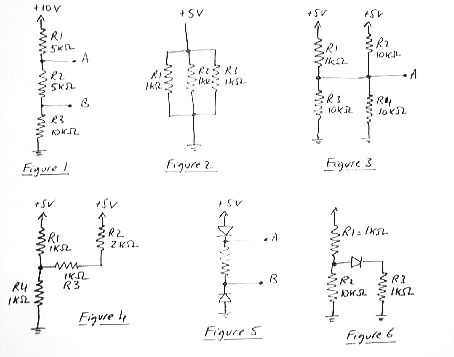
    V = RI
    5 = (5+5+10)K * I = 20K I ==> I = 5/20K = 1/4 mA = current through
                                                       the 3 resistors
    Vb = VR3 = 10K * 1/4 = 2.5 V
    Va = 5 - VR1 = 5 -  5K * 1/4m = 15/4 V

Problem 2

In the circuit of Figure 2, what is the resistor equivalent to the three resitors R1, R2, and R3. Do not simply use the equation we saw in class, but rather derive it, and apply it.

     5 = Req * I0 where Req is the equivalent resistor, and I0 the
         current flowing from +5 to Gnd.
     5 = R1*I1 = R2*I2 = R3 * I3
     and since R1=R2=R3, then I1=I2=I3.  
     
     I0 = I1+I2+I3 = 3 I3.

     Req & 3* I3 = R3 * I3

     Req = R3 /3 = 1/3 KOhm

Problem 3

In the circuit of Figure 3, what is the voltage at Point A (i.e. between Point A and ground)?

Let's find the resistor R' equivalent to the top two resistors (1K and 10K):

1/1 + 1/10 = 1/R' ==> R' = 10/11 K

Let's find the resistor R" equivalent tot he bottom two resistors (10K and
10K)

1/10 + 1/10 = 1/R" ==> R" = 5K

Total current flowing from +5 to ground = I = 5 /(5+10/11).

==> Va = 5 * 5/(5+10/11) = 55/13 Volts

Problem 4

In the circuit shown in Figure 4, what is the voltage across R4? What is the current flowing through R1? Through R2? Through R3? Through R4?

Let's replace R2 and R3 by an equivalent resistor R': R'=2+1 = 3 KOhm
Let's now replace R' and R1 by their equivalent resistor R":

        1/1 + 1/3 = 1/R" ==> R" = 3/4 KOhm

Now the circuit is simpler:
                                 +5V
                                 |
                                 <
                                 > R=3/4 K
                                 <
                                 |
                                 +--------
                                 <
                                 > R4=1K
                                 <
                                 |
                                 |
                                ---

Simply apply Ohm's law and find VR4 = 1K * (5/(3/4+1)) = 20/7 Volts
I1 = (5-20/7) / 1K = 15/7 mA

I4 = 20/7 / 1K = 20/7 mA

I4 is also I1 + I2, so I2 = I4 - I1 = 20/7-15/7 = 5/7 mA

Problem 5

What is the current flowing through the 10 KOhm resistor shown in Figure 5? What is the current through the same resistor, when its value is 0 Ohm (i.e. we replace the resistor by a wire)?

Because the bottom diode is blocking, no current is passing through this
circuit, independently of the value of the resistor.

Problem 6

What is the current flowing through R1 in the circuit shown in Figure 6? Through R2? Through R3? What is the voltage across R2?

Here are the equations we have to deal with and solve:

VR2 = VR3 + 0.5V, since the diode is passing.
VR2 + VR1 = 5
I1 = I2 + I3, where I2 goes through R2, and I3 through R3.
VR1 = 1K * I1
VR2 = 10K * I2
VR3 = 1K * I3

which yield:

   I2 = 5.5/21 = 0.262 mA
   I3 = (105-60.5)/21 = 2.12 mA
   I1 = 2.38 mA

   VR2 = 2.62 V
   VR3 = 2.12 V
   VR1 = 2.38 V

And we verify that VR2 = VR3 + 0.5, and that VR1 + VR2 = 5.