CTMS: MATLAB Basics Tutorial

MATLAB Basics Tutorial

Vectors
Functions
Plotting
Polynomials
Matrices
Printing
Using M-files in MATLAB
Getting help in MATLAB

Key MATLAB Commands used in this tutorial are: plot polyval roots conv deconv inv eig poly

MATLAB is an interactive program for numerical computation and data visualization; it is used extensively by control engineers for analysis and design. There are many different toolboxes available which extend the basic Functions of MATLAB into different application areas; in these tutorials, we will make extensive use of the Control Systems Toolbox. MATLAB is supported on Unix, Macintosh, and Windows environments; a student version of MATLAB is available for personal computers. For more information on MATLAB, contact the MathWorks.

The idea behind these tutorials is that you can view them in one window while running MATLAB in another window. You should be able to re-do all of the plots and calculations in the tutorials by cutting and pasting text from the tutorials into MATLAB or an m-file.

Vectors

Let's start off by creating something simple, like a vector. Enter each element of the vector (separated by a space) between brackets, and set it equal to a variable. For example, to create the vector a, enter into the MATLAB command window (you can "copy" and "paste" from your browser into MATLAB to make it easy):

a = [1 2 3 4 5 6 9 8 7]

MATLAB should return:

     a =
          1  2  3  4  5  6  9  8  7

Let's say you want to create a vector with elements between 0 and 20 evenly spaced in increments of 2 (this method is frequently used to create a time vector):

t = 0:2:20

     t =
          0  2  4  6  8  10  12  14  16  18  20

Manipulating vectors is almost as easy as creating them. First, suppose you would like to add 2 to each of the elements in vector 'a'. The equation for that looks like:

b = a + 2

     b =
          3  4  5  6  7  8  11  10  9

Now suppose, you would like to add two vectors together. If the two vectors are the same length, it is easy. Simply add the two as shown below:

c = a + b

     c =
          4  6  8  10  12  14  20  18  16

Subtraction of vectors of the same length works exactly the same way.

Functions

To make life easier, MATLAB includes many standard functions. Each function is a block of code that accomplishes a specific task. MATLAB contains all of the standard functions such as sin, cos, log, exp, sqrt, as well as many others. Commonly used constants such as pi, and i or j for the square root of -1, are also incorporated into MATLAB.

sin(pi/4)

ans =

     0.7071

To determine the usage of any function, type help [function name] at the MATLAB command window.

MATLAB even allows you to write your own functions with the function command.

Plotting

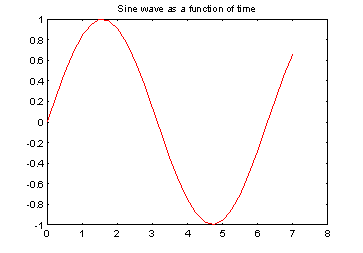
It is also easy to create plots in MATLAB. Suppose you wanted to plot a sine wave as a function of time. First make a time vector (the semicolon after each statement tells MATLAB we don't want to see all the values) and then compute the sin value at each time.

t=0:0.25:7;
y = sin(t);
plot(t,y)

The plot contains approximately one period of a sine wave. Basic plotting is very easy in MATLAB, and the plot command has extensive add-on capabilities.

Polynomials

In MATLAB, a polynomial is represented by a vector. To create a polynomial in MATLAB, simply enter each coefficient of the polynomial into the vector in descending order. For instance, let's say you have the following polynomial:

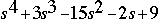
To enter this into MATLAB, just enter it as a vector in the following manner

x = [1 3 -15 -2 9]

     x =
          1  3  -15  -2  9

MATLAB can interpret a vector of length n+1 as an nth order polynomial. Thus, if your polynomial is missing any coefficients, you must enter zeros in the appropriate place in the vector. For example,

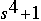
would be represented in MATLAB as:

y = [1 0 0 0 1]

You can find the value of a polynomial using the polyval function. For example, to find the value of the above polynomial at s=2,

z = polyval([1 0 0 0 1],2)

     z =
          17

You can also extract the roots of a polynomial. This is useful when you have a high-order polynomial such as

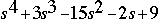
Finding the roots would be as easy as entering the following command;

roots([1 3 -15 -2 9])
        

     ans =
        -5.5745
         2.5836
        -0.7951
         0.7860

Let's say you want to multiply two polynomials together. The product of two polynomials is found by taking the convolution of their coefficients. MATLAB's function conv that will do this for you.

x = [1 2];
y = [1 4 8];
z = conv(x,y)

     z =
          1  6  16  16

Dividing two polynomials is just as easy. The deconv function will return the remainder as well as the result. Let's divide z by y and see if we get x.

[xx, R] = deconv(z,y)

     xx =
          1  2

     R =
          0  0  0  0

As you can see, this is just the polynomial/vector x from before. If y had not gone into z evenly, the remainder vector would have been something other than zero.

Matrices

Entering matrices into MATLAB is the same as entering a vector, except each row of elements is separated by a semicolon (;) or a return:

B = [1 2 3 4;5 6 7 8;9 10 11 12]

     B =
          1    2    3     4
          5    6    7     8
          9   10   11    12

B = [ 1  2  3  4
      5  6  7  8
      9 10 11 12]

     B =
          1    2    3     4
          5    6    7     8
          9   10   11    12

Matrices in MATLAB can be manipulated in many ways. For one, you can find the transpose of a matrix using the apostrophe key:

It should be noted that if C had been complex, the apostrophe would have actually given the complex conjugate transpose. To get the transpose, use .' (the two commands are the same if the matrix is not complex).

Now you can multiply the two matrices B and C together. Remember that order matters when multiplying matrices.

D = B * C

     D =
         30    70   110
         70   174   278
        110   278   446

D  = C * B

     D =
        107   122   137   152
        122   140   158   176
        137   158   179   200
        152   176   200   224

Another option for matrix manipulation is that you can multiply the corresponding elements of two matrices using the .* operator (the matrices must be the same size to do this).

E = [1 2;3 4]
F = [2 3;4 5]
G = E .* F


     E =
          1   2
          3   4

     F =
          2   3
          4   5

     G =
          2   6
         12  20

If you have a square matrix, like E, you can also multiply it by itself as many times as you like by raising it to a given power.

If wanted to cube each element in the matrix, just use the element-by-element cubing.

You can also find the inverse of a matrix:

X = inv(E)

     X =
        -2.0000    1.0000
         1.5000   -0.5000

or its eigenvalues:

eig(E)

     ans =
        -0.3723
         5.3723

There is even a function to find the coefficients of the characteristic polynomial of a matrix. The "poly" function creates a vector that includes the coefficients of the characteristic polynomial.

p = poly(E)

p =

    1.0000   -5.0000   -2.0000

Remember that the eigenvalues of a matrix are the same as the roots of its characteristic polynomial:

roots(p)


     ans =
         5.3723
        -0.3723

Printing

Printing in MATLAB is pretty easy. Just follow the steps illustrated below:

Macintosh

To print a plot or a m-file from a Macintosh, just click on the plot or m-file, select Print under the File menu, and hit return. Windows

in the window of the plot or m-file

Unix

print -P<printername>

print plot.ps

plot.ps" If you are using a HP workstation to print, you would instead use the command "lpr -d plot.ps"

To print a m-file, just print it the way you would any other file, using the command "lpr -P <name of m-file>.m" If you are using a HP workstation to print, you would instead use the command "lpr -d plot.ps<name of m-file>.m"

Using M-files in MATLAB

There are slightly different things you need to know for each platform.

Macintosh

ATLAB

Windows

ATLAB

Unix

ATLAB

You can either type commands directly into MATLAB, or put all of the commands that you will need together in an m-file, and just run the file. If you put all of your m-files in the same directory that you run MATLAB from, then MATLAB will always find them.

Getting help in MATLAB

MATLAB has a fairly good on-line help; type

commandname

for more information on any given command. You do need to know the name of the command that you are looking for.

Here are a few notes to end this tutorial.

You can get the value of a particular variable at any time by typing its name.

You can also have more that one statement on a single line, so long as you separate them with either a semicolon or comma.

Also, you may have noticed that so long as you don't assign a variable a specific operation or result, MATLAB with store it in a temporary variable called "ans".