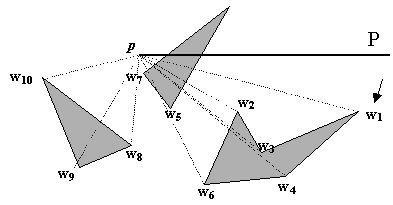
Our naïve algorithm checks for intersection for all pairs of vertices against all obstacles edges. However, there will be economy if we check for intersection in a certain order. In this algorithm, we check if other vertices are visible to a vertex by their cyclic order around that vertex. The best way to illustrate this algorithm will be to give an example of the execution for a certain vertex.
Step 1 : For a certain point p, sort all obstacle vertices according to he clockwise angle that the half-line from p to each obstacle vertex makes with the positive x-axis.

Step 2 : Let P be the half-line parallel to the positive x-axis starting at p. Find the obstacle edges, ei, that are properly intersected by P, and store them in a balanced search tree T (shown right below) in the order in which they are intersected by P. This step takes O(n).
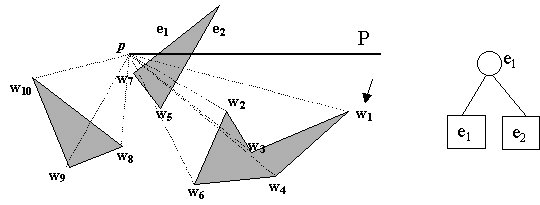
Step 3 : for all vertices wi where i = 1 to n
| 1. | if pwi intersects the interior of the obstacle of which wi is a vertex then return false |
| 2. | else if i = 1 or wi-1 is not on the segment pwi |
| 3. |
|
| 4. |
|
| 5. |
|
| 6. |
|
| 7. |
|
| 8. |
|
| 9. |
|
| 10. |
|
The consequences of this step on w1 is that lines 2-4 of VISIBLE gets executed because i = 1 and ei in T intersects pw1. w1 is not visible from p. This step takes O(log n) time because of search on the binary tree.
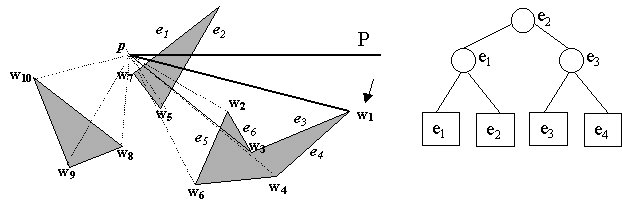
We now turn to w2. The consequences of this step on w2 is that lines 2-4 gets executed because w1 is not on the segment pw2, and that pw2 intersects e1. w2 is not visible from p.
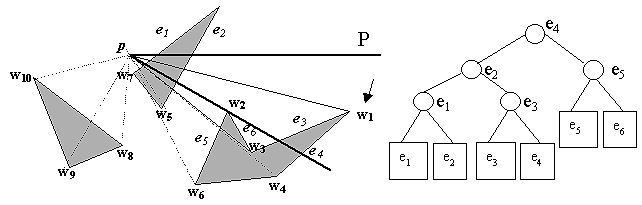
At w3, something interesting happens. e6 and e3, which are incident to w3 on the counterclockwise side of the half-line from p to w3, are deleted from T, the binary tree.
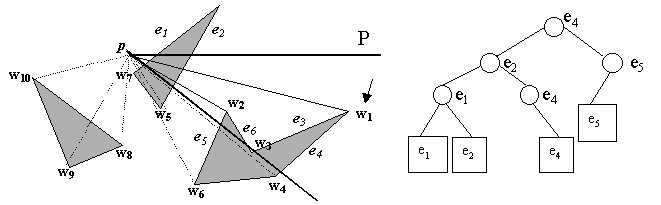
Similarly, at w4, e4 is deleted from T while e7 is inserted into T.
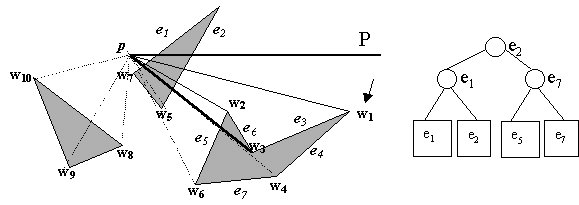
This algorithm goes on until all the run for w10 has finished. This algorithm allows the storage of the obstacle edges that will possibly intersect the next pwi pair. It therefore does not search for all obstacle edges unnecessarily. Moreover, these edges are stored in a binary search tree, so even if all obstacle edges are potential candidates, searching for one that does intersect will only cost O(log n). Lines 6-10 of VISIBLE deals with special cases when wi-1 is on the segment pwi, that is, p, wi-1 and wi are collinear. I do not intend to go into the details, which can be found in M. deBerg et al, 1997. My purpose here to convince you that this algorithm runs in O(n2 log n) time.
The
most time-consuming step in the run for each vertex p is the sorting
of obstacle vertices around p by angularity, which takes O(n
log n). Since we repeat all this process for each of n vertex of
the set of obstacles, the overall runtime is O(n2
log n).