Errata: The Geometry of Spacetime

I wish to express my thanks to David Griffel, University of Bristol, John Chiasson, University of Tennessee, Joseph North, George Mason University, Bill Rozzi, and Alison Duren-Sutherland (Smith '02) for corrections and helpful comments about the text.

Corrections are marked in red, where possible.

Page 6, line +8. ``(t, x, y)'' should be `` $(t, \textcolor{red}{y, z})$''.

Page 14. Exercise 1. The coordinate expression for the first event is missing its closing parenthesis. It should read $(1, 0\textcolor{red}{)}$.

Page 21. Exercise 2 (b). The second equality in the second sentence is incorrect and must be deleted. The corrected sentence should read ``Show that $F_v = S_v \circ C_v$, where S_v is the Galilean shear of velocity v.''

Page 47. Exercise 4. The subscript of the second matrix should be u₂, not u₁. The beginning of the question should read ``Show that $H_{u_1} \cdot H_{\textcolor{red}{u_2}} = \ldots$.''

Page 140. Exercise 5. The first integral in the displayed formula should contain the derivative of $\mathbb{X}$:

$$l = \int_a^b \Vert \mathbb{X\textcolor{red}{'}} (q) \Vert dq ... ...\frac{dz}{dq}\right)^2 - \left(\frac{dt}{dq}\right)^2} \ dq.$$

Page 258, line -2. The word ``and'' within the quotes should be ``an'': ``raising or lowering an index.''

Page 271, line -4. A differentiation prime is missing; the expression should read `` $\mathbf{Q}'(u) = \mathbf{q}\textcolor{red}{'}(\varphi(u)) \varphi'(u) = \mathbf{q}'(t) \varphi'(u)$.''

Page 429. A factor e² is missing from terms in the third and the fifth displayed equations. The third equation should read

$$\frac{d^2v}{d \theta^2} + v = \frac{3\mu^3}{J^4}\left(1 + \fr... ...2}\mu^3}{2J^4} \cos{2\theta} + O\!\left(\frac{1}{c^2}\right).$$

The fifth equation should read

$$v_A = \frac{3\mu^3}{J^4}\left(1 + \frac{e^2}{2}\right), \qqua... ...v_C = - \frac{\textcolor{red}{e^2}\mu^3}{2J^4} \cos{2 \theta}.$$

Page 433, Exercise 6 (b). The error on page 429 is repeated here. The expression C needs to have the factor e² added:

$$C = \frac{3\textcolor{red}{e^2}\mu^3}{2J^4} \cos{2 \theta}.$$

The following errors in the first edition have been corrected in the second printing (August 2001).

Page 27. The displayed formulas for $\tau$ and for E at the top of the page are wrong. They should be

$$\begin{align*}\tau &= \frac{\textcolor{red}{t - v z}}{\sqrt{1 - v^2}}, \\ E(t, ... ...t - v z}}{\sqrt{1 - v^2}}, \frac{z - v t}{\sqrt{1 - v^2}} \right). \end{align*}$$

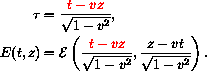
Page 28. Exercise 5. The formula for E(t, z) must be changed as on page 27.

Page 89, line +8. Add the word "does": the total momentum does not change over time:

Page 137. Replace all the text from Proposition 3.4 up to, but not including, Definition 3.7 by the following.

It is evident that the left-hand side--and thus the right--has the dimensions of a rate of change of energy with respect to time. The following proposition will lead us to a physical interpretation for $\mathbf{f} \cdot \mathbf{v}$.

Proposition 3.4 If $\widetilde{K}(t) = \tfrac{1}{2}\mu v^2(t)$ is the classical kinetic energy of G in R's frame and $\mathbf{\tilde{f}} = \mu \mathbf{a}$ is the classical 3-force  acting on G, then

$$\dfrac{d\widetilde{K}}{dt} = \mathbf{\tilde{f}} \cdot \mathbf{v}.$$

PROOF: Since $v^2 = \mathbf{v} \cdot \mathbf{v}$, we can write $\widetilde{K}(t) = \dfrac{\mu}{2} \mathbf{v} \cdot \mathbf{v}$. Therefore,

$$\frac{d\widetilde{K}}{dt} = \frac{\mu}{2} (\mathbf{v} \cdot \... ... \mathbf{v}. \tag*{\mbox{}\hfill\mbox{\textsc{end of proof}}}$$

Let us therefore interpret $\mathbf{f} \cdot \mathbf{v}$ (which involves the relativistic 3-force f) as the time rate of change of relativistic kinetic energy K of G in R's frame. Thus $\mathbb{F}\cdot \mathbb{U} = 0$ becomes

$$c^2 \, \dfrac{dm}{dt} = \frac{dK}{dt}, \quad \text{implying} \quad c^2 m = K + \text{const}.$$

If we further require that K = 0 when v = 0, as in the classical case, then we can determine the constant of integration in the last equation: Since $m = \mu$ and K = 0 when v = 0, it follows that $\text{const} = \mu c^2$, the rest energy  of G. We can summarize the previous discussion in the following definition and corollary.

Page 138, line 4. Insert between ``K'' and the colon:

We also have an expression for the relativistic kinetic energy Kthat agrees with the one we used in section 3.1 for non-accelerated motion:

Page 190, line -4. Insert the sentence: ... $hN = h\nu - h\nu \Delta \Phi$. (For the rest of this paragraph, hrepresents Planck's constant, not the position of C.) If we let...

Page 244. In the figure, the Gauss image $\mathcal{G}(\alpha)$ in S¹ is incorrect; it should be rotated $90^\circ$ counterclockwise, as in the figure below.

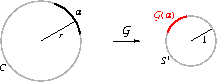
Page 268. The statement about the normal component N of acceleration (and the formula given in line -4) are incorrect, as is the displayed formula immediately above that line. The displayed formula and the sentence following it should read

$$\left( \frac{d^2 q^k}{dt^2} + \Gamma_{ij}^k \frac{d q^i}{dt... ... \textcolor{red}{\frac{d q^i}{dt}\frac{d q^j}{dt}} \mathbf{n}.$$

The last term is the normal component N of acceleration. It depends on the second fundamental form b_ij and the velocity components dqⁱ/dt of the curve z(t), but is in general different from zero.

Page 375, line -1. Add a space between `` $\delta_k^h$'' and ``is''.

Page 382. In exercise 9 (c), two minus signs are missing. The statement should read:

Assume $T_{ij} \equiv 0$ and show that $R = \textcolor{red}{-}4 \Lambda$ where R is the scalar curvature function R = R_iⁱ. Then show that $R_{ij} = \textcolor{red}{-} \Lambda g_{ij}$.

Page 431, The paragraph ``Visualizing the drift'' states incorrectly the size of the drift due to the other planets. Replace the paragraph with the following.

In fact, most of the shift is due to the fact that the observations are made in a non-inertial frame; only about one-tenth is due to the Newtonian gravitational ``disturbances by other planets.'' The relativistic contribution is extremely small; even over 80 centuries it amounts to just under $1^\circ$, but it is enough to be visible in the figure on the next page. By contrast, the observed shift during the same time is enormous--a third of a complete revolution. The figure is drawn to scale and gives an accurate picture of the eccentricity of Mercury's orbit. The non-relativistic contribution (of about 5557'' per century) is shown by the dashed ellipse, the correct (relativistic) drift by the gray ellipse.

About this document ...

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 -no_navigation errata.tex.

The translation was initiated by Jim Callahan on 2002-04-30